Abstract

The objective of this paper is to investigate and compare the timbre representation potential of the STFT and the Wigner Distribution in the context of timbre morphing. Both Time-Frequency distributions can be interpreted as the energy in time and frequency of a signal. There are however, intrinsic differences between the distributions. The Wigner distribution of multi-component signals exhibits cross terms, while the STFT representation inherently involves  smearing in both time and frequency directions. However, the Wigner distribution cross terms can be reduced through the use of an appropriate smoothing window, thereby providing the basis for improved timbre feature analysis and processing.
 
 

1     Introduction

Of the elements of musical composition, timbre has, at least until modern times, been the most neglected.  The musical potential inherent in timbre manipulation has, of course, been realized for centuries but for the greater part this has been regarded as a subtlety best left to the performer as he/she sought to enhance their musical expression.  Only with the development of electronic processing devices has timbre come to be regarded as a true compositional element which can be brought under specifiable control for musical effect.  It is almost certainly the case that those compositions to date which rely heavily on timbre variations (e.g. works by Stockhausen, Boulez and others) for effect are but the warp and weft of a tapestry which has yet to be revealed, and that, as timbre processing becomes easily available to mainstream composers through  the development of effective tools for 'timbre manipulation', it is likely that the utility and effectiveness of timbre as a medium for composition will become fully apparent.  It might be suggested that our current situation regarding the development of tools for the exploitation of timbre as a compositional element may be compared to that of harmony and the development of effective keyboard instruments in the sixteenth century.   With historical hindsight, it is clear that the increasing availability of keyboards at that time allowed relatively easy compositional development of 'vertical blocks' of sound, an aspect which was not so easily conceived or experimented with for the case of string or voice which, for the greater part, demanded ensemble performance of harmonies. As a consequence, the use of harmony as a compositional element 'flowered' following keyboard development.

With the arrival of electronic processing, timbre is now becoming accessible as a compositional element.  Computer synthesis techniques allow both faithful mimicking of  so-called 'natural' tones and artificial generation of new sonorities. To date, the basis for timbre representation and manipulation has been what is referred to as the 'classical' concept of tone quality which relates timbre primarily to its spectral composition, i.e. to the pattern of harmonics inherent in different instrument tones.  However, synthetic processing techniques clearly demonstrate the inadequacy of 'harmonic recipes' for timbre representation.  For example, a piano note played backwards is perceived to have a very different tonal quality from the same note played in its normal sequence, although the spectral composition of both normal and reversed notes is identical.  In short, there is now a very significant body of research evidence which clearly indicates the importance of both spectral and transient or temporal note characteristics for perceived tone.  The significance of these findings for artificial synthesis and ultimately for composition is very noteworthy.

Firstly, it is becoming clear that traditional instruments allow exploration of a very small part of what might be called 'timbre space'.  Secondly, it is evident that computer processing techniques, as are inherent in many digital synthesizers, are not being exploited to the full in that a comprehensive palette of timbres is not typically being made available to the composer/artist.  A more mature approach to timbre processing would be based on what is referred to as 'joint time-frequency distributions' which make both transient and spectral information accessible.  One example of such distributions is the Spectrogram, familiar to those working with speech processing.  However, it can be shown that the Spectrogram is not an optimal joint time-frequency distribution as it introduces significant 'smearing' of temporal and spectral information which can distort, or even hide, both transient and spectral aspects which may be of musical significance.  As a consequence of the realisation of the inadequacies of both the spectrum (i.e. harmonics) and the Spectrogram for timbre representation, attention has been brought to bear on the mathematical foundations of time-frequency distributions in an effort to identify an optimal distribution which would allow accurate representation of both temporal and spectral information.

As a result of such studies the Wigner Distribution, originally developed for joint distribution in Quantum Mechanics, has been applied to signal analysis and its superiority has been established for accurate time-frequency representation.  In the context of the representation of musical timbres, the Wigner Distribution allows accurate analysis of both temporal and spectral details, and thereby facilitates synthetic processing of both transient and steady-state aspects of musical tones.  This in turn opens up previously unexplored vistas in timbre space in that timbre manipulation is not confined to spectral processing.   With an ability to 'see' the full detail of temporal and spectral composition of musical timbres comes the desire to manipulate these same details for the purposes of creative, musical expression.

One approach to the exploration of 'timbre space' is based on the possibilities inherent in 'morphing' between  two chosen timbres.  The concept of visual morphing is familiar to many from 'special effects' processing in cinema.  A good example is where we are shown a young face gradually and smoothly age as it moves from youth to old age.  This is achieved by using two frames - one young and the other old - and manipulating various 'perceptually significant' parameters so that the presented face appears to move from the youthful 'starting' frame to the aged 'finishing' frame.  An exactly analogous process may be applied to musical timbres.  For example, we may choose a violin 'starting' timbre and a flute 'finishing' timbre and manipulate various important (spectral and temporal) features so that we can move smoothly between them.  By so doing we open up new parts of timbre space which nevertheless are not entirely unknown to us in that we would at least be operating between the known boundaries of 'violin' and 'flute', or whatever other timbres we had chosen at the outset.   Thus, morphing would provide the composer with access to a much richer 'timbre palette' than there before, in that previously unexplored regions of timbre space could be made available for creative manipulation.  By basing such morphing tools on Wigner Distributions of musical tones, rather than Spectrograms, representational distortions would be minimized and detailed spectral and temporal features of real instrument tones would be made much clearer for the purposes of computational analysis and synthesis.

When attempting to develop a morphing algorithm, the intrinsic problems involved in the analysis of timbre must first be considered.  That is, the sounds to be morphed must first be analysed to determine those spectral and temporal features which characterise timbre. Then, in the implementation of timbre morphing, a number of problems must be addressed relating to the attempt to smoothly blend two, perhaps very different, 'feature sets'.  The term 'feature' is introduced by Holloway, Tellman and Haken [1] in their description of a timbre morphing algorithm.  A feature is any part of a sound that contributes to its timbre. While, as stated previously, the classical position assigned timbre representation solely to the pattern of harmonic steady state amplitudes, the more modern position gives full acknowledgement to the importance of the details of the temporal evolution of individual harmonics.  Consequently, the feature sets involved in timbre synthesis and morphing require  extraction of both temporal and spectral details. Thus, the accurate extraction of these features from a given timbre representation is possibly the most important step in attaining an effective synthesis of a 'morphed' timbre.  It is the purpose of this paper to present some preliminary results which indicate the superiority of the Wigner Distribution as a joint time-frequency representation which may be used as a basis for timbre morphing.
 
 

2     History of Timbre Representation

Fourier Analysis is a powerful technique for estimating the frequency content of many real signals, including speech and musical tones. The Fourier Transform (FT) of  a non-stationary signal, f(t), is given in equation 1, which allows the generation of a signal spectrum

To allow a greater generality in the study of timbre space it is necessary to combine time-amplitude representations, with frequency-amplitude relationships. This is so as to allow observation of how the spectral components of a musical sound  evolve over time (i.e. how the spectra develop).

The Short-Time Fourier Transform (STFT) or the Spectrogram [2], was originally developed as a time-frequency-intensity representation for speech analysis. It is a simple extension of the FT, where the FT is repeatedly evaluated for a running windowed version of the time domain signal. Each FT gives a frequency domain 'slice' associated with the time value at the window center. The  STFT is represented analytically by

where t indicates the position of the window on the time axis. The Spectrogram can be used for time-frequency analysis of musical tones. It enables us to observe the temporal and spectral characteristics at any point in the 'timbre space'. Slaney, Covell and Lassiter [3] make a point of using Magnitude Spectrograms, which allow changes to be made to the Spectrogram, in the knowledge that the phase will be recovered in the inverse Spectrogram. The simplest case they use for the purpose of morphing involves two quasi-stationery tones. These each have well defined spectral shape, pitch, rhythm, and other perceptually relevant auditory dimensions. For example two different pitches cause sounds to be perceived as two different auditory objects. This is but one of the difficulties faced in performing a successful morph, and in this case, it can be overcome by scaling the frequencies in the STFT which allows interpolation between the different pitches. This, unfortunately, does not work for drastic pitch changes as formants are also moved. Apart from such intrinsic morphing difficulties, it is also the case that other problems arise due to the nature of the joint time-frequency representation used. For example, the Spectrogram has a significant shortcoming in that it involves an intrinsic trade-off between time resolution and frequency resolution. The reason for the time-frequency resolution trade-off is the Fourier domain property that a window and its spectrum cannot both be arbitrarily narrow. The implication is that improvements in the identification of spectral detail from a Spectrogram can only be achieved at the expense of deterioration in temporal resolution. Given that this is not entirely satisfactory in the context of timbre morphing, we are put upon to identify joint time-frequency representations that facilitate better joint time-frequency resolution. One such representation is the Wigner Distribution.

The Wigner Distribution (WD) was proposed by Wigner in 1932 for application in quantum mechanics. It has more recently been recognised as a powerful tool for time-frequency analysis of signals, where with some care, it can be interpreted as a distribution of the signal energy in time and frequency. Claasen and Mecklenbrauker [4] show that the WD can be evaluated from both the time signal f(t)

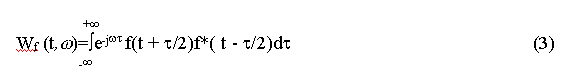
and from the Fourier Transform, F(w), of the time signal f(t)

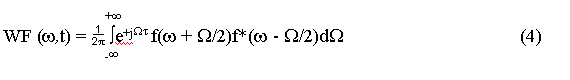
The two distributions have the relation:

It can also be shown that the WD is the most basic or primary time-frequency distribution, as defined by Cohen [5], [6]. In the context of timbre representation, an important attribute is the spread of the square magnitude of any joint time-frequency distribution. We can make our choice among the many distributions of the Cohen class with the simple demand of minimum spread. In the case of the WD, it can be shown that this smearing/spreading will be a minimum and will be greatly reduced in comparison to that of the STFT, hence allowing better feature identification for morphing. While the STFT suffers from the important drawback of improved frequency resolution being obtained only at the expense of time resolution and vice versa, the WD overcomes this drawback. So, the WD minimises the inherent averaging over time and frequency of the STFT, but, as has often been pointed out, at the expense of the introduction of cross products.

Recently, Pielemeier and Wakefield [7] have looked at other time-frequency analysis methods for representation of musical signals, including the constant-Q modal distribution, which can be used as the basis for estimation of temporal and spectral parameters. They dismiss the possibility of using the WD for the representation of musical timbres due to the distortion introduced by the cross terms previously mentioned.  It is the purpose of this paper to show that effective smoothing of the WD can remove the bothersome interference products while still providing minimal spreading of temporal detail.  It is suggested that such smoothed WDs can provide a useful basis for the extraction of those features relevant to timbre morphing.
 
 

3     The Wigner Distribution - theme and variations!

So far, the WD has just been considered for continuous-time signals. To perform a practical computer-based measurement the WD needs to be evaluated from a discrete-time signal. Windowing and sampling the continuous-time signal, Claasen and Mecklenbrauker [8] show that

The new function in equation 6 is the discrete Pseudo Wigner Distribution (PWD). In this case,

· p(k) = w(k)w*(-k) is the window time correlation function, and
· g(n,k) = f(n+k) f*(n-k) is the signal time correlation function.

Here, z(l) is the smoothing window. In general the window length for w(k) is 2L and is therefore reasonably large. The smoothing window length for z(l) is 2m and is generally of short duration, as if it is too large it smoothes too much of the required PWD signal.  It can be shown that the optimum smoothing window type is Gaussian [9].
 
 

4     Graphical Comparison of Spectrograms and Wigner Distributions

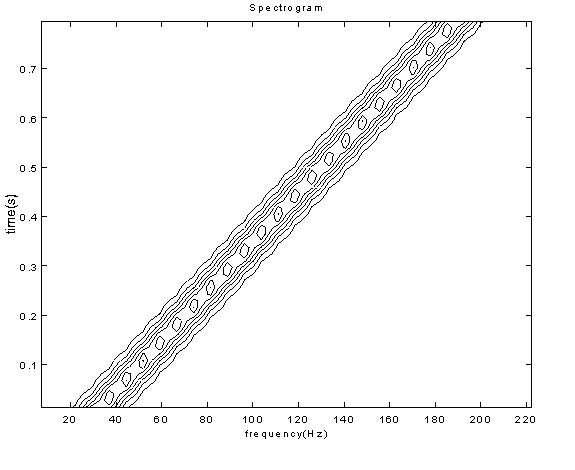
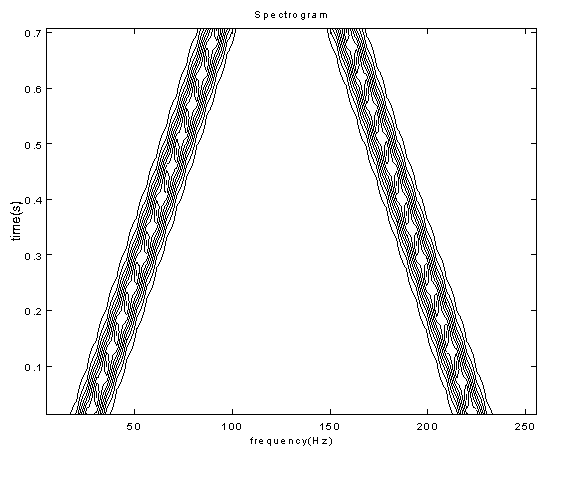
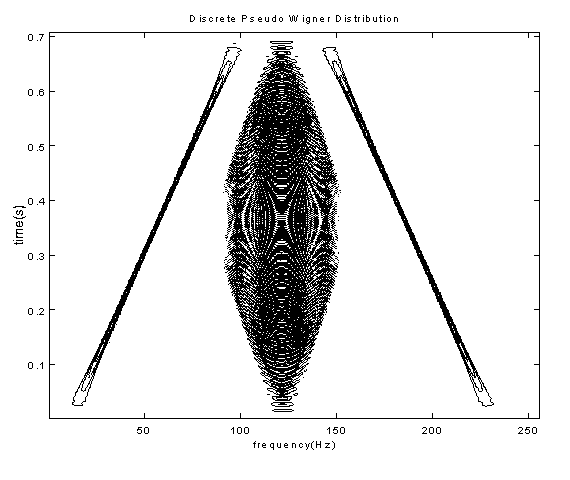
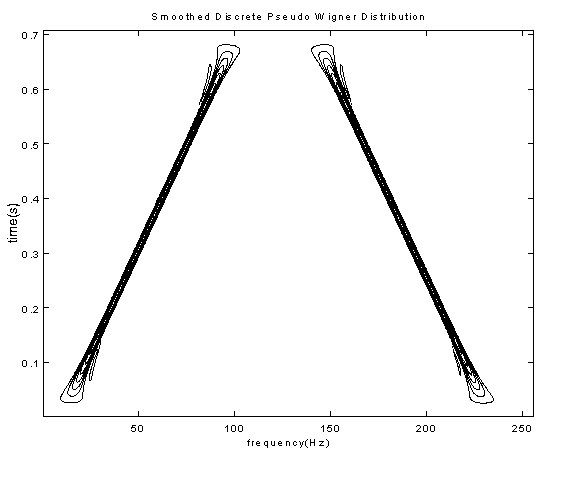
In order to investigate the relative performance of the STFT and WDs with regard to accurate representation of temporal and spectral detail, an examination of a number of synthesized signals has been undertaken. For the purposes of demonstration, particular cases of the STFT and WDs of single and dual chirps and musical signals are presented.  As will be seen, the spreading or smearing of the STFT (fig. 5.1) relative to the WD (fig. 5.2) is very evident for single chirps.  However, when the multi-component dual chirp is used the WD cross terms become all too obvious (fig. 6.2). It is shown that the introduction of a Gaussian smoothing window effectively eliminates this interference (fig. 6.3).

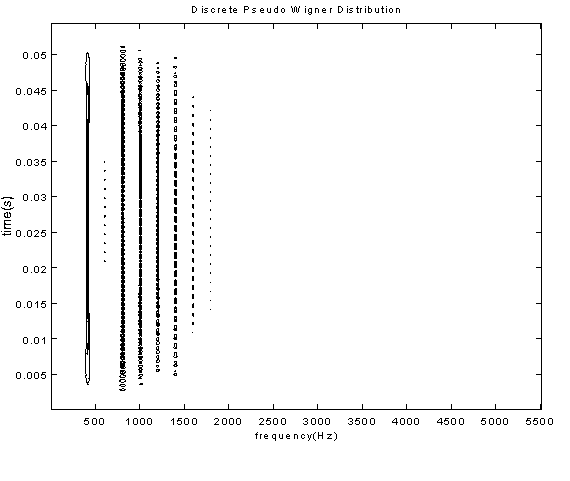
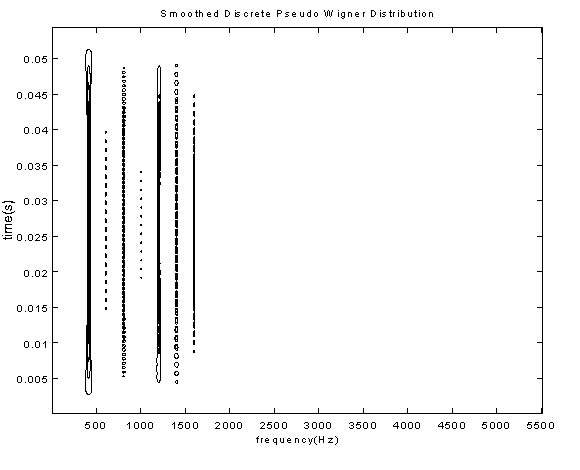
When the SPWD is applied to real musical signals - in this case, the example used in figures 7.1, 7.2 and 7.3 is a portion (0.12s) of the quasi-steady state section of a synthesized tone of fundamental pitch 440Hz, sampled at 5000Hz - the clutter seen in figure 7.2, which previously was the principal objection to the use of the WD for timbre representation, is seen to be absent (fig. 7.3). From this it can be suggested that the spectral and temporal features required for timbre morphing can be more accurately extracted using the SPWD (fig. 7.3) rather than the STFT (fig. 7.1) representation. The analysis of a longer sample should improve the resolution of the STFT, however, the relative superiority of the SPWD would remain. The temporal and spectral smearing of the STFT makes it more difficult to identify the correct location of any of the harmonics in figure 7.3. Each, is smeared over an average range of approximately 185Hz, while each is smeared temporally beyond the extents of the analysis window.  The SPWD of the same tone (fig. 7.3), displays much better spectral resolution than that of the STFT(fig. 7.1), and temporally it remains within the analysis window. Based on these comparisons, over similar analysis window lengths, the PWDF appears to provide for more accurate feature identification - than that provided by the STFT - within the signal.

For example, in relation to a morph between  two quasi-stationary sounds, Slaney, Covell and Lassiter [3] point out that the feature in the first sound needs to be slowly moved to its corresponding position in the second sound during the morphing process, as features have often moved relative location between the sounds. Using the SPWD, it would be much easier to identify any changes in features. This point is all the more important when seen in the light of Iverson and Krumhansl's [10] work, where they showed that although the onset of a tone is not required for similarity judgement between tones, it is required to enable listeners to identify an instrument. In the following, graphical comparisons of the relative performance of the STFT and the WD for the various test signals will be presented.
 
 

5     Single Chirp

PWD

6     Dual Chirp  

STFT

PWD

SPWD

7     Synthetic Tones  

STFT

8     Conclusions

From the analysis presented, and from the graphical presentations given, it is clear that the WD can be used for effective representation of musical timbres.  When appropriate smoothing is applied the cross terms, which introduce unwanted clutter for multi-component signals, can be eliminated at the expense of the introduction of a degree of spectral smearing.  It is notable, however, that, firstly, this smearing is not as significant as that of the Spectrogram, and secondly, that temporal smearing is not introduced.  This is a significant advantage over the STFT which is constrained to a trade-off between temporal and spectral resolution.  For the purposes of musical synthesis deriving from timbre morphing, the increased accuracy of the WD representation will allow more accurate extraction of those features which characterise musical timbre.
 
 
 
 
 
 
 
 
 

9     References

[1] B. Holloway, E. Tellman and L. Haken, "Timbre Morphing of Sounds with Unequal Numbers of Features," J. Audio Eng. Soc. vol. 43, no. 9, pp 678-689, September 1995.

[2] L.R. Rabiner and R.W. Schafer, "Digital Processing of Speech Signals," Prentice-Hall, Englewood Cliffs, NJ  1978.

[3] M. Slaney, M. Covell and B. Lassiter, "Automatic Audio Morphing," in Proc. ICASSP, IEEE, Atlanta, GA, May 7-10, 1996.

[4] T.A.C.M. Claasen and W.F.G Mecklenbrauker, "The Wigner Distribution - A Tool for Time-Frequency Signal Analysis, part 1: Continuous-Time Signals," Phillips Journal of Research, vol. 35, no.3, pp. 217-250, 1980.

[5] L. Cohen, "Generalized Phase-Space Distribution Functions," J. Math. Phys., vol. 7, pp. 781-786, 1966.

[6] L. Cohen and H. Margeneau, "Probabilities in Quantum Mechanics," in Quantum Theory and Reality, M. Bunge, Ed. (Springer, Berlin), chap. 4, pp. 71-89, 1967.

[7] W.J. Pielemeier and G.H. Wakefield, "A high-resolution time-frequency representation for musical instrument signals," J. Acoust. Soc. Am., vol. 99 (4), Pt. 1, pp 2382-2396, April 1996.

[8] T.A.C.M. Claasen and W.F.G Mecklenbrauker, "The Wigner Distribution - A Tool for Time-Frequency Signal Analysis, part 2: Discrete-Time Signals," Phillips Journal of Research, vol. 35, no.4/5, pp. 276-300, 1980.

[9] J.C. Andrieux, R. Feix, G Mourgues, P. Bertrand, B. Izrar and V.T. Nguyen, "Optimum Smoothing of the Wigner-Ville Distribution," IEEE Transactions on Acoustics, Speech and Signal Processing, vol. ASSP-35, no. 6, pp. 764-769, June 1987.

[10] P. Iverson and C.L. Krumhansl, "Isolating the dynamic attributes of musical timbre," J. Acoust. Soc. Am., Vol. 94 (5), pp 2595-2603, November 1993.